Statistics
You should be familiar with basic statistical concepts like measures of central tendency (mean, median, mode), dispersion (standard deviation, variance), and linear regression.
During the MSIS program
A basic understanding of statistics will be helpful in a number of courses in the MSIS program. These concepts will serve as building blocks for more advanced analytics which can be used to make strategic recommendations.
Nice to have
All of these examples can be completed using Excel. Being able to use statistical tools like SPSS, MatLab, or R is a bonus.
Once you have completed the prerequisites for the Computer Programming module, you are encouraged to apply these concepts in Python.
Major concepts
You should be able to do the following:
- Compare and contrast important measures of central tendency and dispersion.
- For a given population sample, calculate mean (\(\bar{x}\)), median, mode, standard deviation (\(s\)), and variance (\(v\)).
- Define linear regression. Describe its uses and limitations.
- Calculate a regression line showing the relationship between two variables.
Nice to have
- Be able to build regression equations given multiple independent variables.
- Correctly apply polynomial (second-order) and logistic regression.
Resources
-
It is important to understand central tendency in data. This article by Laerd Statistics is a good read for a formal definition of central tendency and its measures. It also compares these measures by application.
-
This introductory Statistics course module from Khan Academy has simple examples of mean, median and mode. (~15 mins)
-
This video on Standard Deviation explains central tendency with an example. Watch this video on standard deviation to learn how standard deviation is calculated.
-
Dispersion is a measure of how wide or narrow a bell curve is, and is communicated using variance* or standard deviation**. This Variance & Standard Deviation course module from Khan Academy teaches measures of dispersion in statistics. (~25 minutes)
-
The free online course “Introduction to Statistics” is an excellent resource.
-
This book provides a remarkably fun way to learn the basics of statistics:
Head First Statistics: A Brain-Friendly Guide, 1st Ed., Dawn Griffiths, O’Reilly Media (2018), ISBN-13: 978-0596527587 [Amazon]
Linear regression
- Linear Regression is a statistical method for data analysis that models a relationship between a dependent variable and one or more independent variables. It is used to either predict an unknown value (dependent variable) given a set of features (independent variables).
For example, let’s say we have a dataset of three variables: height, weight, and gender. We could try to predict weight based on height and gender, or we could try to predict height based on the remaining variables.
-
Nuts & bolts of linear regression -
- Dependent variable (\(\hat{y}\)): The unknown variable we are trying to predict the value of. It is always continuous and numerical.
- Independent variable (\(x\)): Known variable(s) used to predict \(\hat{y}\).
- Regression equation: The mathematical equation that represents the regression model \(\hat{y} = a + bx\) (for simple linear regression), where \(a\) is the y-intercept and \(b\) is the slope (also call “correlation coefficient”).
- Simple linear regression: Regression using a single independent variable.
- Multiple linear regression: Regression using two or more independent variables.
-
It’s important you to be able to do linear regression.
-
Linear regression should only be used when the use case is appropriate. This article by Eric Benjamin Seufert nicely explains good and bad candidates for linear regression.
-
The article “A Refresher on Regression Analysis” from Harvard Business Review is another good read. It explains how companies use regression, and the common mistakes people make when using it.
Practice
There are many free data sets suitable for use in learning statistics. The “Data and Story Library” has good sets for practicing confidence intervals and regression. If you’re practicing in R, this collection of sample datasets originally distributed with R may prove useful.
If you want more interesting data sets (with no guarantee of suitability for practice), Jeremy Singer-Vine at Data Is Plural publishes a weekly newsletter of interesting data sets (archive).
First, try the exercises below using Excel. Then try the same exercises using some other statistical or programming tool, like SPSS, R or Python.
Exercises
-
In a normal distribution, what percent of the sample population is within one standard deviation of the mean? What percent is within two standard deviations? Three?
Answer
For data having a symmetric, normal distribution:
- Approximately 68% of the data is within one standard deviation of the mean
- Approximately 95% of the data is within two standard deviations of the mean
- More than 99% of the data is within three standard deviations of the mean
For skewed data, the percentages are different, but are still within boundaries described by Chebyshev's Rule
-
Use this “Body Fat” dataset. Use weight as the dependent variable.
- Describe the mean, median, and mode for weight.
Answer
Hint: Use the Analysis ToolPak Add-in to quickly get descriptive statistics in Excel.
Statistic Value Mean 178.1 Median 176.1 Mode 184.25 Std Dev 27.1 Std Variance 730.9 Count 250 - Describe the standard deviation (\(s\)) and variance (\(v\)) of weight. Explain what they mean. What is the relationship between standard deviation and variance?
- What are the Excel functions to calculate population standard deviation (\(\sigma\)) and sample standard deviation (\(s\))?
- Using words, describe the bell curve for weight. Graph the bell curve; evaluate your description.
Answer
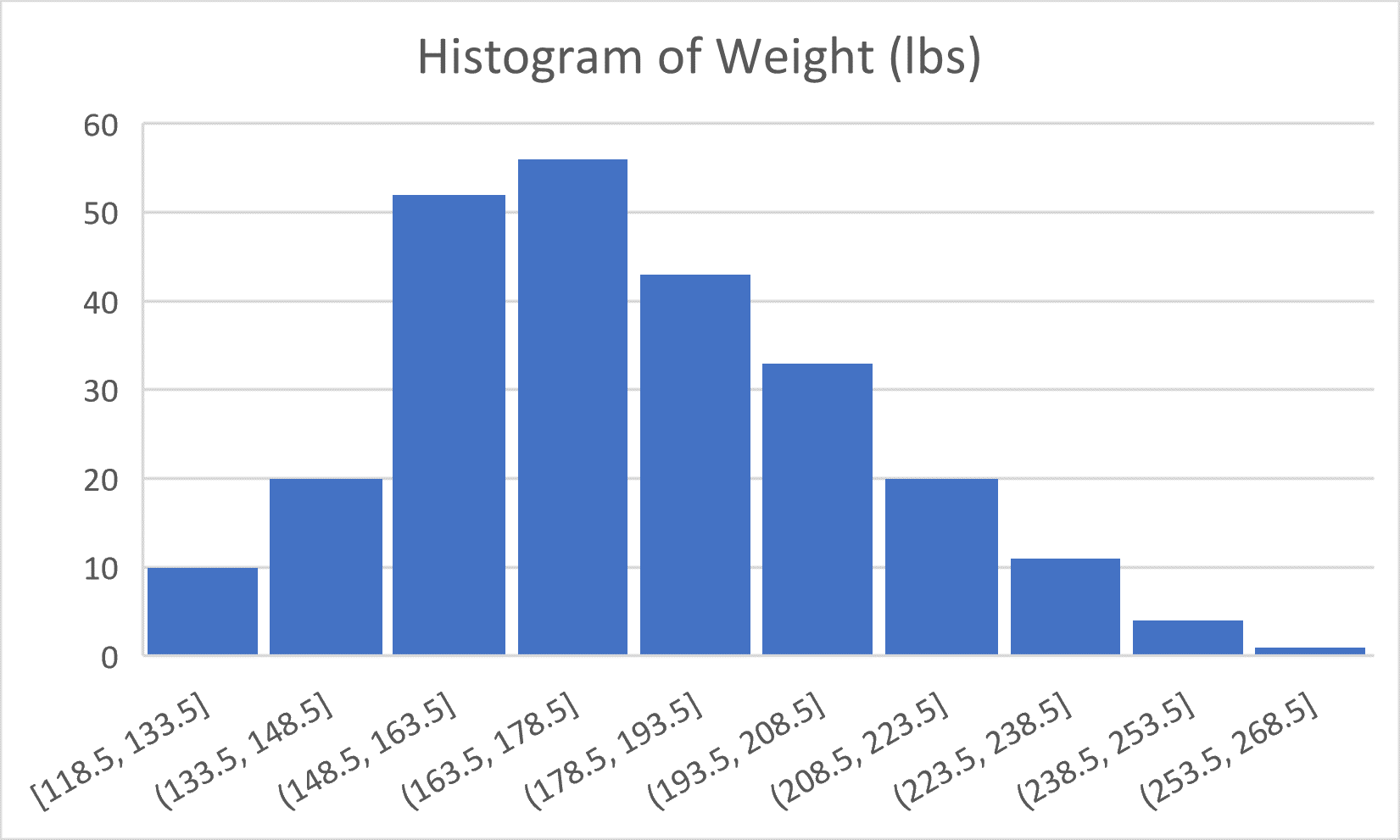
- Regress weight by height. What is the coefficient and y-intercept? Does the equation make sense?
Answer
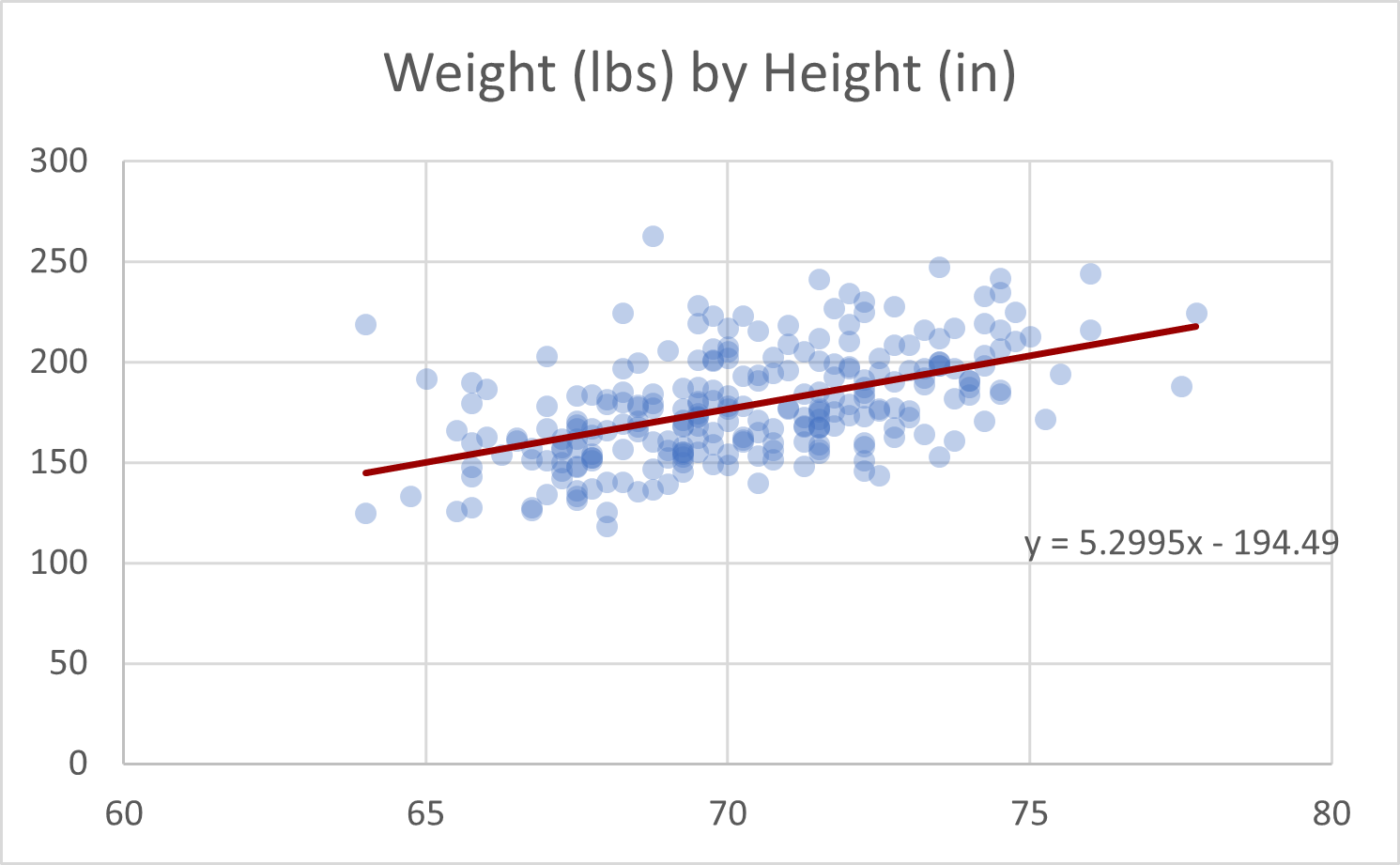
Coefficient of height: 5.3 (In other words, every inch of height typically adds about 5.3 pounds.)
Intercept: -194.4861343
Full equation: \(predicted\ weight = 5.3*height - 194.5\)
\(R^2\): 0.263 (This equation explains only about 26% of the variance in weight.) - OPTIONAL: Regress weight by multiple variables. Which variables best predict weight? How do you decide?
- Describe the mean, median, and mode for weight.